Tag: backtesting
-
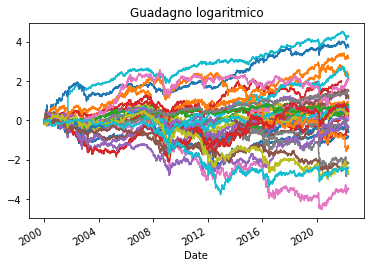
Buy & Hold la stretegia vincente
Ho analizzato il comportamento di un paniere di titoli per vederne il comportamento complessivo nel tempo. In particolare già in passato avevo analizzato la strategia buy & hold verificando che è difficile trovare una strategia di trading migliore di quella B&H. Con l’occasione ho voluto sperimentare backtesting alternativi rispetto a Backtrader. Credo che Backtrader sia…
-
Studio della regressione lineare applicata ai titoli
Tra i diversi indicatori non si trovano spesso indicatori basati sulla regressione lineare, che a mio avviso ha alcuni aspetti interessanti di applicazione. Dati lineari o logaritmici La regressione lineare può essere applicata per interpolare i dati di chiusura del mercato e individuare un trend di mercato. L’approccio può essere considerato simile a quelli di…
-
Comportamento indicatore SuperTrend
L’indicatore SuperTrend è uno degli indicatori che mi piace maggiormente, prima di scoprirne e conoscerne l’esistenza ho costruito in modo simile, ne condivido i razionali sottostante. Non entro sui dettagli implementativi e mi limito a studiarne il comportamento nel suo utilizzo. L’indicatore è di tipo trend-following, l’aspetto che lo rende interessante è che non usa…
