Categoria: Fintech
-

GenAI e Normative: come si muove la comunità Europea
Oggi (13 febbraio) il comitato europeo sull’intelligenza artificiale dovrebbe approvare un nuovo regolamento in materia Intelligenza Artificiale che sarà successivamente votato dal parlamento Europeo nel mese di marzo per diventare legge europea. Sono i passi finali di un percorso iniziato nel 2022 Il testo approvato già in bozza il 2 febbraio 2024 per l’Atto sull’Intelligenza…
-

rocm e una calcolatrice con rete neurale
Circa sei mesi fa, per esigenze di gaming di mio figlio, ho deciso di cambiare la scheda video e già che c’ero ho pensato di comprarne una che sia supportata come acceleratore negli apprendimenti di machine learning tra cui keras. Potevo scegliere una scheda Nvidia con cuda, come la precedente, ma ho optato per una…
-

Sostenibilità di blockchain e LLM
Nell’era della digitalizzazione, due tecnologie emergenti, i modelli di intelligenza artificiale come i modelli LLM e le blockchain Proof of Work (PoW), si trovano al centro di un cruciale dilemma etico legato alla sostenibilità e alla poca trasparenza sull’impronta di carbonio generata. Quanto consumano i sistemi LLM La quantità esatta di risorse di calcolo richieste…
-
LSTM & le false promesse
Di recente mi sono imbattuto in un articolo che mostra come l’applicazione si tecniche di ML basate su LSTM possano generare risultati migliori rispetto a una strategia B&H. La prima osservazione è che il singolo titolo non fa testo, occorre avere un paniere sufficientemente ampio per dimostrare che un algoritmo di ML sia efficace. Subito…
-
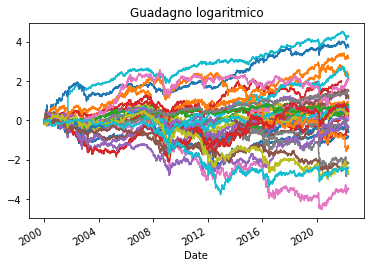
Buy & Hold la stretegia vincente
Ho analizzato il comportamento di un paniere di titoli per vederne il comportamento complessivo nel tempo. In particolare già in passato avevo analizzato la strategia buy & hold verificando che è difficile trovare una strategia di trading migliore di quella B&H. Con l’occasione ho voluto sperimentare backtesting alternativi rispetto a Backtrader. Credo che Backtrader sia…
