Tag: errore quadratico medio
-
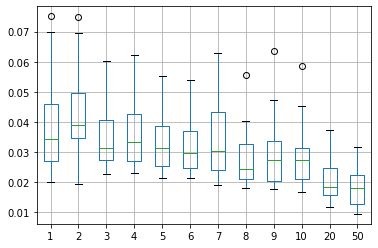
Tuning rete neurale
Ho iniziato a sperimentare le reti neurali con il framework pyhton keras e dopo le prime prove mi sono reso conto che l’attività di tuning di una rete neurale è molto delicata. Quanti nodi servono? Quanti livelli? I batch quanto devono essere grossi? E sopratutto quante epoche di trainng servono? Come prima attività di tuning…
